Kampfsystem (Civ4): Unterschied zwischen den Versionen

Version vom 20. Juni 2007, 10:31 Uhr

Dieser Artikel wird gerade überarbeitet. Eine aktualisierte Version wird in Kürze zur Verfügung stehen.

Allgemeines

Ein Kampf besitzt folgende Eigenschaften:

• Er läuft in Runden ab
• Es sind genau 2 Einheiten beteiligt : 1 Angreifer (A) und 1 Verteidiger (V)
• Er endet immer mit den Tod einer Einheit

(Ausnahme: Angreifer mit Rückzugfähigkeit können bei einer Niederlage flüchten)

• Jede Einheit startet mit x Trefferpunkten (Tp) in den Kampf, wobei x := {1,2,3,4,...,97,98,99,100}.
• Ist eine Einheit verletzt (d.h. x < 100 TP ), so wirkt sich das dirket auf den Stärkewert der Einheit aus.
• Sein Verlauf steht in direkter Abhängigkeit von der Gesamtstärke der jeweiligen Einheiten.
• Während des Kampfes ist die Gesamtstärke konstant.

Notation

• [math]a[/math] := Angreifer
• [math]v[/math] := Verteidiger
• [math]S_a[/math]:= Sollstärke des Angreifers, wobei [math]S_a \in \mathbb{N}[/math].
• [math]B_a[/math]:= Boni des Angreifers, wobei [math]B_a \in \mathbb{N}[/math].
• [math]M_a[/math]:= Mali des Angreifers, wobei [math]M_a \in \mathbb{N}[/math].
• [math]G_a[/math]:= Gesundheit des Angreifers, wobei [math] G_a \in [1,100] \subset\mathbb{N}[/math].
• [math]E_a[/math]:= Anzahl der Erstschläge des Angreifers, wobei [math]E_a \in \mathbb{N}[/math].

• [math]S_v[/math]:= Sollstärke des Verteidigers, wobei [math]S_v \in \mathbb{N}[/math].
• [math]B_v[/math]:= Boni des Verteidigers, wobei [math]B_v \in \mathbb{N}[/math].
• [math]M_v[/math]:= Mali des Verteidigers, wobei [math]M_v \in \mathbb{N}[/math].
• [math]G_v[/math]:= Gesundheit des Verteidigers, wobei [math] G_a \in [1,100] \subset\mathbb{N}[/math].
• [math]E_v[/math]:= Anzahl der Erstschläge des Verteidigers, wobei [math]E_a \in \mathbb{N}[/math].

Vorberechnungen

Berechnung von Ist-Gesamtstärke und Soll-Gesamtstärke

Als erstes wird die Istgesamtstärke für den Angreifer und den Verteidiger berechnet (Schreibweise: [math]I_a\,\text{bzw}\,I_v\,)[/math]:

[math] I_a = \left{\begin{array}{cl} S_a\, \left( 1 %2B+ \frac{B_a - M_a}{100} \right)\, \cdot \, \frac{G_a}{100}\,, & \mbox{wenn}\,B_a - M_a \geq 0 \\ S_a \, \left(1 %2B+ \left|\frac{B_a - M_a}{100}\right|\right)^{-1}\, \cdot \, \frac{G_a}{100}\,, & \mbox{wenn}\,B_a - M_a\lt 0 \end{array}\right [/math]

[math] I_v = \left{\begin{array}{cl} S_v\, \left( 1 %2B+ \frac{B_v - M_v}{100} \right)\, \cdot \, \frac{G_v}{100}\,, & \mbox{wenn}\,B_v - M_v \geq 0 \\ S_v \, \left(1 %2B+ \left|\frac{B_v - M_v}{100}\right|\right)^{-1}\, \cdot \, \frac{G_v}{100}\,, & \mbox{wenn}\, B_v - M_v\lt 0 \end{array}\right [/math]

Die Ist-Gesamtstärke hängt von den jeweiligen Boni und Mali ab sowie von der aktuellen Gesundheit. Ist die Differenz von Boni und Mali größer als Null, wird die große Klammer mit der Stärke multipliziert, ist die Differenz kleiner als Null, wird die Stärke durch die große Klammer dividiert.

Anschließend wird die Soll-Gesamtstärke für den Angreifer und den Verteidiger berechnet (Schreibweise: [math] \mathfrak{S}_a\,\text{bzw.}\,\mathfrak{S}_v[/math]):

[math] \mathfrak{S}_a = \left{\begin{array}{cl} S_a\, \left( 1 %2B+ \frac{B_a - M_a}{100} \right)\,, & \mbox{wenn}\,B_a - M_a \geq 0 \\ S_a \, \left(1 %2B+ \left|\frac{B_a - M_a}{100}\right|\right)^{-1}\,, & \mbox{wenn}\,B_a - M_a\lt 0 \end{array}\right [/math]

[math] \mathfrak{S}_v = \left{\begin{array}{cl} S_v\, \left( 1 %2B+ \frac{B_v - M_v}{100} \right)\,, & \mbox{wenn}\,B_v - M_v \geq 0 \\ S_v \, \left(1 %2B+ \left|\frac{B_v - M_v}{100}\right|\right)^{-1}\,, & \mbox{wenn}\, B_v - M_v\lt 0 \end{array}\right [/math]

Die Sollgesamtstärke hängt hier nur von den Boni und Mali ab, nicht aber von der Gesundheit. Ist die Differenz von Boni und Mali größer als Null, wird die große Klammer mit der Stärke multipliziert, ist die Differenz kleiner als Null, wird die Stärke durch die große Klammer dividiert.

Folgendes ist dabei zu beachten:

• Die Beförderungen Kampf I-VI werden grundsätzlich zu dem eigenem Stärkewert addiert.

• Feldjäger I + II, Gebirgsjäger I + II und Stadtverteidigung I-III kommen nur bei Verteidigungseinheiten zum tragen.

• Ausfall, Deckung, Formation, Gebirgsjäger III, Hinterhalt, Schock, Speerfeuer II + III, Stadtangriff I-III und Zangenangriff: Deren Auswirkungen hängen immer von der IST-Stärke des Verteidigers ab.

• Einheitenfähigkeiten (xxx% geg. Einheitentyp/Gelände): Deren Auswirkungen hängen immer von der IST-Stärke des Verteidigers ab.

Beispiel: Schwertkämpfer (A) besitzt Rang I und Bogenschütze (V) Rang II. (Beide bei voller Gesundheit) Gesamtstärke (A) = 6 * 1,10 = 6,60 Gesamtstärke (V) = 3 * 1,20 = 3,60

Beispiel: Ein verletzter Speerkämpfer (V) mit einer IST-Stärke von 2, wird in einem Wald von einem berittenen Bogenschützen (A) mit einer IST-Stärke von 6, und der die Beförderungen Rang I und Schock bezitzt, angegriffen:

Für den Angreifer: IST-Stärke (A) = 6 * 1,10 (+10% Stärke) * 100/100 = 6,60 (Schock wird hier nicht dazu gezählt)

Für den Verteidiger: [Summe aller Boni] - [Summe aller Mali] = 1,5 - 0,25 = 1,25 > 0

Daraus folgt Fall a):

Gesamtstärke (V) = 2 * ( 1 + 0,5 (+50% Waldbonus) + 1,00 (+100% gegen berittene Einheiten) – 0,25 (-25% wegen Schock) = 2 * 2,25 = 4,50

Feuerkraft (Neu ab Patch 1.61)

Als nächstes berechnen wir die Feuerkraft. Sie ist erst seit dem Patch 1.61. für Vanillia dabei und wird ist das arithmetische Mittel aus der Ist-Gesamtstärke und der Soll-Gesamtstärke (Schreibweise: [math]F_a\,\mbox{bzw}\, F_v[/math]):

[math]F_a = \frac{I_a %2B+ \mathfrak{S}_a}{2} [/math]

[math]F_v = \frac{I_v %2B+ \mathfrak{S}_v}{2} [/math]

Beispiel: Für den ber. Bogenschützen ergibt sich eine Feuerkraft von:

(6,60 + 6,60) / 2 = 6,60 (welch Überraschung)

Für den Speerkämpfer:

(4,50 + 9,00) / 2 = 6,75

Zu beachten ist, dass das Ergebnis immer auf die 2.Dezimalstelle abgerundet wird.

Schaden pro Runde

Jetzt berechnen wir, wie viel Schaden eine Einheit pro Kampfrunde verursachen kann. Dazu bestimmen wir den Angriffswert des Angreifers und des Verteidigers (Schreibweise: [math]\mathfrak{A}_a \,\mbox{bzw}\,\mathfrak{A}_v[/math]):

[math]\mathfrak{A}_a = 20\,\cdot\, \frac{3\,\cdot\,F_a %2B+ F_v}{3\,\cdot\,F_v%2B+F_a} [/math]

[math]\mathfrak{A}_v = 20\,\cdot\, \frac{3\,\cdot\,F_v %2B+ F_a}{3\,\cdot\,F_a%2B+F_v} [/math]

Beispiel: Für den ber. Bogenschützen ergibt sich: Schaden/Runde (A) = 19 TP Für den Speerkämpfer ergibt sich: Schaden/Runde (V) = 20 TP

Benötigte Treffer zum Sieg (BT)

Als nächstes kommt die Berechnung der Anzahl an Kampfrunden dran, die eine Einheit maximal überstehen kann, eher sie den Kampf verliert. Dabei ist diese Anzahl stark abhängig von der momentanen Gesundheit der jeweiligen Einheit, ebenso spielt die Angriffskraft eine Rolle (Schreibweise:[math] R_a \,\mbox{bzw}\, R_v [/math]):

[math] R_a = \frac{G_a}{\mathfrak{A}_v} [/math]

[math] R_v = \frac{G_v}{\mathfrak{A}_a} [/math]

Beispiel: Für den ber. Bogenschützen ergibt sich: BT = 3 Für den Speerkämpfer ergibt sich: BT = 5

Die Wahrscheinlichkeit, eine Kampfrunde zu gewinnen

Als letzte Vorberechnung kommt jetzt die Wahrscheinlichkeit, dass der Angreifer bzw. der Verteidiger eine Kampfrunde gewinnt (Schreibweise: [math] p_a \,\mbox{bzw}\, p_v [/math]):

[math] p_a = \frac{I_a}{I_a %2B+ I_v} [/math]

[math] p_v = \frac{I_v}{I_a %2B+ I_v} [/math]

Es gilt [math] p_a %2B+ p_v = 1 [/math].

Mit den Vorberechnungen sind wir jetzt fertig. Für die eigentlichen (schwierigeren) Berechnungen brauchen wir die Werte für die Anzahl an Kampfrunden, bis der Angreifer bzw. der Verteidiger verlieren, sowie die Wahrscheinlichkeit, mit der eine Kampfrunde verloren wird.

Berechnung der endgültigen Siegeschance ( ohne Erstschlag)

Es gibt 2 mögliche Ereignisse:

- E1: „Der Speerkämpfer gewinnt“ oder „Der ber. Bogenschütze verliert“ - E2: „Der ber. Bogenschütze gewinnt“ oder „Der Speerkämpfer verliert“

Im Folgenden wird das Ereignis E1 betrachtet:

Der Speerkämpfer gewinnt den Kampf, wenn er von 7 Runden 5 gewinnt und verliert ihn, wenn er 3 Runden verliert. Die Wahrscheinlichkeit, mit der er eine Runde gewinnt, beträgt p(V)=0,41. Der Kampf endet, sobald er 5 Treffer erzielt, sein 5. Treffer muss auch der letzte sein. (Danach ist der Gegner tot.)

Mögliche Ergebnisse können sein:

1. Der Speerkämpfer gewinnt 5 von 5 Runden (Er trifft immer, der ber. Bogenschütze nie)
2. Der Speerkämpfer gewinnt 5 von 6 Runden (Der ber. Bogenschütze trifft einmal)
3. Der Speerkämpfer gewinnt 5 von 7 Runden (Der ber. Bogenschütze trifft zweimal)

Die dazugehörigen Wahrscheinlichkeiten werden mit Hilfe der Binominalverteilung berechnet: P(X) = B(n; k; p)

n = Anzahl an stattfindenden Runden k = Anzahl an Runden, die gewonnen werden müssen p(V) = Wahrscheinlichkeit, mit der eine Runde gewonnen wird

P(1) = B(5; 5; 0,41) = 0.0110 P(2) = B(5; 4; 0,41) * 0,41 = 0.0326 P(3) = B(6; 4; 0,41) * 0,41 = 0.0581

Wieso eigentlich B(5; 4; 0,41) * 0,41 und nicht B(6; 5; 0,41)? Da der letzte Treffer vom Speerkämpfer kommen muss, sind weniger Möglichkeiten gegeben, wie der Kampf ablaufen kann. Bei B(6; 5; 0,41) gibt es 6 mögliche Anordnungen, bei B(5; 4; 0,41) * 0,41 nur 5 (wegen n!/(k!*(n-k)!)).

Die Gesamtsiegeswahrscheinlichkeit P(E1) ist die Summe aller Unterwahrscheinlichkeiten.

P(E1) = P(1) + P(2) + P(3) + P(4) = 10.2%

Der Speerkämpfer geht mit einer Wahrscheinlichkeit von 10.2% siegreich aus dem Kampf hervor.

Erstschläge

Was sind Erstschläge? Erschläge sind im Prinzip Freirunden, in denen eine Einheit angreifen kann, ohne im Falle einer Niederlage befürchten zu müssen, verletzt zu werden. Erstschläge laufen vor dem eigentlichen Kampf ab. Theoretisch könnte bei einer ausreichend hohen Anzahl an verfügbaren Erstschlägen der Kampf gewonnen werden, ohne dass der Feind die Möglichkeit zur Gegenwehr hätte.

Während eines Kampfes kann entweder nur eine Einheit über Erstschläge verfügen oder überhaupt keine. Beide gleichzeitig ist unmöglich. Wenn also der Angreifer A x-Erstschläge und der Verteidiger V y-Erstschläge verfügen, so gibt die Differenz x-y = e darüber Aufschluss, welcher Fall eintritt:

1) Für e > 0 --> A verfügt über Erstschläge 2) Für e < 0 --> V verfügt über Erstschläge 3) Für e = 0 --> Weder A noch V verfügen über Erstschläge

Verschiedene Einheiten besitzen schon von Natur aus eine bestimmte Anzahl an verfügbaren Erstschlägen. Durch die Erstschlags-Beförderungen (wie sie seit Warlords heißen) kann die Anzahl erhöht werden. Erstschlag I + III bilden eine Ausnahme, sie erhöhen nur die Chance, Erstschläge zur Verfügung zu bekommen. Z.B. gibt Erstschlag I 0-1 Erstschläge.

Wichtig: Die Wahrscheinlichkeit, einen Erstschlag zu erhalten, ist p = 50%.

Beispiel: Bogenschütze (V) Schwertkämpfer (A)

(V) : - Boni: +50% Waldbonus / +10% durch Rang I - SOLL-Stärke 3 - SOLL-Gesamtstärke 4,8 - IST-Stärke 2,5 - IST-Gesamtstärke 4 - 2 Erstschläge

(A) : - keine Boni - SOLL-Stärke = IST-Stärke = SOLL-Gesamtstärke = IST-Gesamtstärke = 6

Zitat: Zitat von Tzu Iop Also um das Ganze zu berrechnen brauchen wir auf jeden Fall die Binominalverteilung.

Also was wissen wir über die Szenarios in denen der Bogi gewinnt: 1. Das letzte Ereignis muss ein Treffer des Bogis sein. 2. Der Bogi muss 7mal getroffen haben, um den Schwerti zu besiegen. 3. Der Kampf endet nach dem 7. Treffer des Bogis.

Damit haben wir alle wichtigen Infos. Außerdem vereinfachen wir die Sache erstmal, wir gehen davon aus das der Bogi _keine_ Erstschläge hat.

p = 0,4

a) Bogi gewinnt 7 von 7 Runden, sprich er trifft immer, der Schwerti nie.

B (7; 0,4; 7) = 0,0016...

b) Bogi gewinnt 7 von 8 Runden.

B (7; 0,4; 6) * 0,4 = 0,0069...

Die meisten denken jetzt warum so und nicht B (8; 0,4; 7). Ganz einfach das letzte Ereignis muss ja ein Treffer des Bogis sein. Deshalb sind nur die Ereignisse davor in der Reihenfolge variabel. Wenn man B (8; 0,4; 7) berrechnen würde, würde man auch die Möglichkeit berrechnen, dass der Schwerti in Runde 8 den Bogi verletzt. Diese Möglichkeit exestiert jedoch nicht, da davor bereits 7 Treffer vom Bogi stehen und damit der Kampf schon zu Ende sein muss.

c) 7 von 9 Runden

B (8; 0,4; 6) * 0,4 = 0,01652...

d) 7 von 10 Runden

B (9; 0,4; 6) * 0,4 = 0,02973...

e) 7 von 11 Runden

B (10; 0,4; 6) * 0,4 = 0,04459...

Also Gesamtchance ist dann: 0,0016 + 0,0069 + 0,01652 + 0,02973 + 0,04459 = 0,09934 = 9,934%

Das war jetzt ohne Erstschläge das ganze jetzt nochmal mit. 0 Erstschlagserfolg ist ja identisch mit keine Erstschläge; wird also nicht nochmal berechnet.

1 Erstschlagserfolg:

B(6; 0,4; 6) = 0,0040 B(6; 0,4; 5) * 0,4 = 0,0147 B(7; 0,4; 5) * 0,4 = 0,0310 B(8; 0,4; 5) * 0,4 = 0,0495 B(9; 0,4; 5) * 0,4 = 0,0669

Summe: 16,61%

2 Erstschlagserfolge:

B(5; 0,4; 5) = 0,0102 B(5; 0,4; 4) * 0,4 = 0,0307 B(6; 0,4; 4) * 0,4 = 0,0553 B(7; 0,4; 4) * 0,4 = 0,0774 B(8; 0,4; 4) * 0,4 = 0,0929

Summe: 26,65%

Endgültig für 4 mit 2 Firststrike gegen 6: 9,934% * 0,36 + 16,61% * 0,48 + 26,65% * 0,16 = 15,83%

Das sollte jetzt endgültig richtig sein, es sei denn ich habe mich irgendwo verrechnet. Und hier die Wahrscheinlichkeit, dass der Schwertkämpfer gewinnt.

Zitat: Zitat von Tzu Iop Gleiche Regeln. P = 0,6

0 Erstschläge:

B (5; 0,6; 5) = 0,0778 B (5; 0,6; 4) * 0,6 = 0,1555 B (6; 0,6; 4) * 0,6 = 0,1866 B (7; 0,6; 4) * 0,6 = 0,1742 B (8; 0,6; 4) * 0,6 = 0,1393 B (9; 0,6; 4) * 0,6 = 0,1003 B (10; 0,6; 4) * 0,6 = 0,0669

Summe: 0,9006 = 90,06%

1 Erstschlag:

B (5; 0,6; 5) = 0,0778 B (5; 0,6; 4) * 0,6 = 0,1555 B (6; 0,6; 4) * 0,6 = 0,1866 B (7; 0,6; 4) * 0,6 = 0,1742 B (8; 0,6; 4) * 0,6 = 0,1393 B (9; 0,6; 4) * 0,6 = 0,1003

Summe: 0,8337 = 83,37%

2 Erstschläge:

B (5; 0,6; 5) = 0,0778 B (5; 0,6; 4) * 0,6 = 0,1555 B (6; 0,6; 4) * 0,6 = 0,1866 B (7; 0,6; 4) * 0,6 = 0,1742 B (8; 0,6; 4) * 0,6 = 0,1393

Summe: 0,7334 = 73,34%

Endwahrscheinlichkeit: 90,06% * 0,36 + 83,37% * 0,48 + 73,34% * 0,16 = 84,17%

9,934% + 90,06% = 99,994% 16,61% + 83,37% = 99,98% 26,65% + 73,34% = 99,99%

15,83% + 84,17% = 100,00%

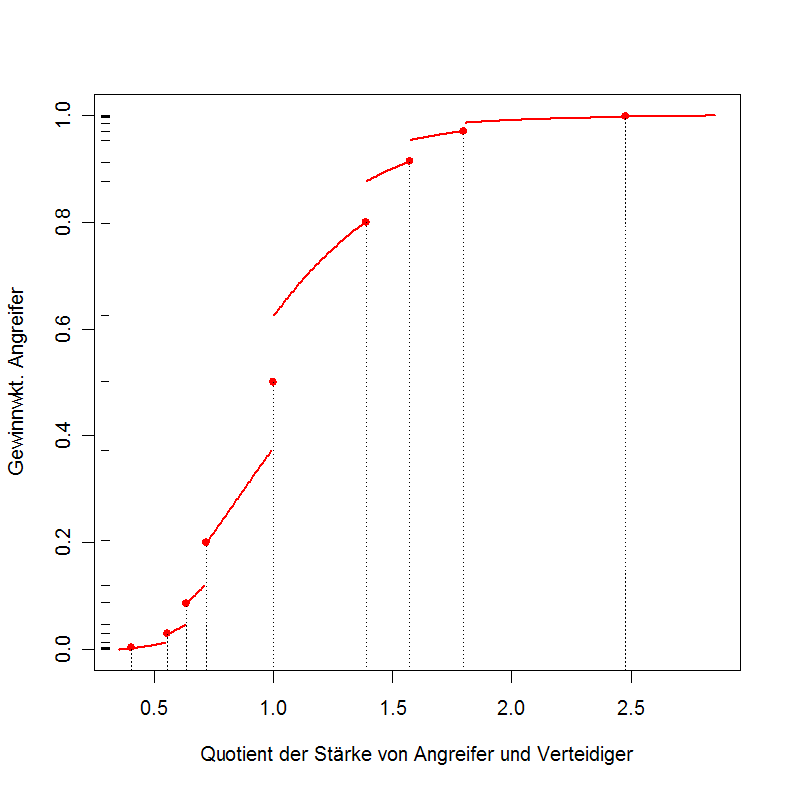
Das Prinzip der "Sprünge"

Man betrachte einen Kampf zwischen zwei gleichstarken Einheiten ( (A) und (V) ). Es sollen folgende Situationen betrachtet werden:

1. (A) erhält keine Rang-Beförderung 2. (A) erhält Rang I 3. (A) erhält Rang II 4. (A) erhält Rang III 5. (A) erhält Rang IV 6. (A) erhält Rang V 7. (A) erhält Rang I und +25% gegen Einheitentyp 8. (A) erhält Rang II und +25% gegen Einheitentyp

Die dazu gehörigen Siegwahrscheinlichkeiten P(E) von (A) sind:

P(1) = 50,00% P(2) = 68,01% P(3) = 72,87% P(4) = 76,98% P(5) = 87,88% P(6) = 90,06%

P(7) = 79,64% P(8) = 90,06%

P(4) = P(7) ( ungefähr) P(6) = P(8)

Bei P(2) (Rang I) und bei P(5) (Rang IV) kommt es zu "Sprüngen". Dazu kommt es, weil sich sich die [Benötigten Treffer zum Sieg] des Verteidigers erhöhen.