Kampfsystem (Civ4): Unterschied zwischen den Versionen
K (→Feuerkraft (Neu ab Patch 1.61): Klammern) |
(Begriffsklärungslink) |
||
| (54 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Kategorie:Civ4]] | [[Kategorie:Civ4]] | ||
| − | {{ | + | [[Kategorie:Spielkonzept (Civ4)]] |
| + | {{Begriffskl | | ||
| + | text = Dieser Artikel erläutert das Kampfsystem in ''Civilization IV''. Für das gleichnamige Spielkonzept in anderen Teilen der Civilization-Reihe siehe [[Kampfsystem]]. | ||
| + | }} | ||
| + | |||
== Einführung == | == Einführung == | ||
| Zeile 36: | Zeile 40: | ||
#Eine Einheit kann befördert werden. Die meisten Beförderungen geben Boni auf bestimmte Kampfbedingungen, z.B. gibt die Beförderung Schock einer Einheit einen +25% Bonus gegen Nahkampeinheiten. | #Eine Einheit kann befördert werden. Die meisten Beförderungen geben Boni auf bestimmte Kampfbedingungen, z.B. gibt die Beförderung Schock einer Einheit einen +25% Bonus gegen Nahkampeinheiten. | ||
| − | |||
| − | |||
| − | + | == Vorberechnungen== | |
| − | + | ||
| + | |||
| + | === Kampfmodifikatoren === | ||
| + | |||
| + | Einheiten können mit bestimmten Beförderungen ihre Kampfkraft verbessern. Auch spielt das Gelände, wo der Kampf ausgetragen wird, eine große Rolle. Nachfolgend werden alle Modifikatoren aufgelistet, die den Kampf beeinflussen (jeweils für den Angreifer und für den Verteidiger): | ||
| − | |||
| − | |||
| − | |||
| − | + | '''Modifikatoren, die auf den Angreifer wirken''' | |
| − | * | + | *Kampf I-VI |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''Modifikatoren, die auf den Verteidiger wirken''' | |
| − | |||
| − | |||
| − | |||
| − | |||
| + | *''Kampf I-VI'' | ||
| + | *''Angriff'', ''Deckung'', ''Finte'', ''Formation'', ''Hinterhalt'', ''Schock'' | ||
| + | *''Häuserkampf I-III'' | ||
| + | *''Garnison I-III'' | ||
| + | *''Guerilla I-III'', ''Waldkampf I-III'' | ||
| + | *''Speerfeuer II-III'' | ||
| + | *Gelände: Hügel, Wald, Fluss (falls Angreifer ohne Beförderung ''Amphibisch''), Amphibische Landung (falls Angreifer ohne Beförderung ''Amphibisch'') | ||
| + | *Verschanzung und Kulturverteidigung | ||
| + | *Diverse Einheitenfähigkeiten | ||
| − | + | Im folgendem steht <math>B_a</math> für die Boni, die der Angreifer bekommt, und <math>B_v,\, M_v</math> steht für die Boni bzw. Mali, die der Verteidiger bekommt. | |
| + | Der Angreifer selbst wird niemals Mali bekommen. | ||
| − | + | (Beispiele hierfür im nächsten Abschnitt.) | |
=== Berechnung von Ist-Gesamtstärke und Soll-Gesamtstärke === | === Berechnung von Ist-Gesamtstärke und Soll-Gesamtstärke === | ||
| − | + | '''Definition''' | |
| + | |||
| + | Seien <math>S_a,\,S_v \in\mathbb{N}</math> die ''Sollstärke'' des Angreifers bzw. des Verteidigers, <math>B_a,\,B_v\in\mathbb{N}_0</math> seien die ''Boni'' des Angreifers bzw. des Verteidigers, <math>M_v\in\mathbb{N}</math> sei die ''Mali'' des Verteidigers, <math>G_a,\,G_v\in\,[1,100]\subset\mathbb{N}</math> seinen die ''Gesundheitwerte'' des Angreifers bzw. des Verteidigers. | ||
| + | |||
| + | |||
| + | Dann werden '''Soll-Gesamtstärke''' <math>\mathfrak{S}</math> und '''Ist-Gesamtstärke''' <math>I</math> des Angreifers bzw. des Verteidigers wie folgt berechnet: | ||
| + | |||
| + | |||
| + | |||
| + | *Für den Angreifer: <math> \quad\mathfrak{S}_a:=S_a\, \left( 1 + \frac{B_a}{100} \right) </math> | ||
| + | |||
| + | |||
| + | *Für den Verteidiger: <math> \quad \mathfrak{S}_v:= | ||
| + | \left\{ | ||
| + | \begin{array}{cl} | ||
| + | S_v\, \left( 1 + \frac{B_v - M_v}{100} \right) \,, & \mbox{falls} \,B_v - M_v \geq 0 \\ | ||
| + | S_v\, \left( 1 + \frac{M_v - B_v}{100} \right)^{-1} \,, & \mbox{falls}\, B_v - M_v < 0 | ||
| + | \end{array} | ||
| + | \right\} </math> | ||
| + | |||
| + | |||
| + | *Für den Angreifer: <math>\,\, \quad I_a:= \mathfrak{S}_a\,\cdot\,\frac{G_a}{100} </math> | ||
| + | *Für den Verteidiger: <math> \quad I_v:=\mathfrak{S}_v\,\cdot \, \frac{G_v}{100} </math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''Bemerkung''': | ||
| − | + | Mit '''Sollstärke''' ist die Stärke gemeint, die eine Einheit bei ihrer Errichtung besitzt. Zum Beispiel besitzt ein Bogenschütze eine '''Sollstärke''' von 3. (Anders ausgedrückt ist mit '''Sollstärke''' die Stärke gemeint, die eine Einheit bei voller ''Gesundheit'' besitzt.) | |
| + | Die '''Sollstärke''' ist immer eine natürliche Zahl, die Null ist nicht dabei (deswegen auch die Schreibweise <math>S_a,\,S_v \in\mathbb{N}</math>). | ||
| + | (Zur Erinnerung: Natürliche Zahlen sind: <math>1,2,3,4,...</math>) | ||
| + | Die '''Boni''' und '''Mali''' nehmen ebenfalls nur Werte aus den nathürlichen Zahlen an, diesmal aber mit der Null (deswegen auch die Schreibweise <math>B_a,\,B_v\in\mathbb{N}_0</math>). | ||
| − | + | Die '''Gesundheit''' nimmt Werte aus den natürlichen Zahlen von 1 bis 100 an (deswegen die Schreibweise <math>G_a,\,G_v\in\,[1,100]\subset\mathbb{N}</math>). Ein Wert von 100 bedeutet volle '''Gesundheit''' einer Einheit, und dadurch bedingt auch volle Stärke. Ein Wert von 0 bedeutet, dass die Einheit vernichtet ist. (Vernichtete Einheiten können nicht mehr kämpfen, deswegen wird hier der Wert 0 als '''Gesundheitswert''' nicht zugelassen.) | |
| − | + | Die '''Soll-Gesamtstärke''' des Angreifers hängt von der ''Sollstärke'' des Angreifers und von dessen ''Boni'' ab. Je größer die ''Sollstärke'' oder die ''Boni'' sind, desto größer ist die '''Soll-Gesamtstärke'''. | |
| − | + | Sind keine ''Boni'' vorhanden, dann entspricht die '''Soll-Gesamtstärke''' gerade der ''Sollstärke''. | |
| + | Für den Verteidiger gilt das gleiche, nur kommen noch die ''Mali'' dazu. | ||
| + | Es müssen hier 2 Fälle unterschieden werden. Ist die Differenz aus ''Boni'' und ''Mali'' positiv, so wird die ''Sollstärke'' mit der Klammer (aus der Formel oben) '''multipliziert'''. Ist die Differenz negativ, so wird die ''Sollstärke'' durch die Klammer '''dividiert'''. | ||
| + | Je größer also die ''Mali'', desto kleiner die '''Soll-Gesamtstärke'''. | ||
| − | |||
| − | |||
| − | Die | + | Die '''Ist-Gesamtstärke''' unterscheidet sich von der ''Soll-Gesamtstärke'' nur derart, dass nun auch die ''Gesundheit'' ein Parameter ist. Ist der Wert der ''Gesundheit'' gleich 100, so entspricht die '''Ist-Gesamtstärke''' gerade der ''Soll-Gesamtstärke''. Je geringer die ''Gesundheit'' ist, desto geringer ist auch die '''Ist-Gesamtstärke'''. |
| − | ==== | + | ====Beispiel 1==== |
| − | |||
| − | + | Ein unverletzter '''Krieger''' mit den Beförderungen ''Kampf I'' (+10% Stärke) und ''Deckung'' (+25% gegen Bogenschützen) will einen ebenfalls unverletzten, aber unbeförderten '''Bogenschützen''' auf offenem Gelände angreifen. | |
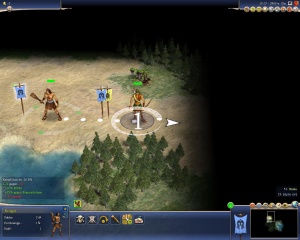
| + | [[Bild:Modi10000.JPG|thumb|Im Fenster links unten über dem Kriegerbild kann man gut erkennen, wie die Beförderungen ''Kampf I'' und ''Deckung'' des Kriegers wirken. | ||
| + | Dabei stehen die Zahlen <span style="color:#228B22">'''2.2'''</span> und <span style="color:#ff0000">'''2.4'''</span> für die Ist-Gesamtstärke des Kriegers bzw. des Bogenschützens.]] | ||
| + | Für die Soll-Gesamtstärke und Ist-Gesamtstärke des Kriegers gilt: | ||
| − | |||
| − | * | + | *<math> \quad\mathfrak{S}_a=S_a\, \left( 1 + \frac{B_a}{100} \right) = 2\,\cdot\,\left(1 + \frac{10}{100}\right) = 2.2</math> |
| − | + | *<math> \quad I_a= \mathfrak{S}_a\,\cdot\,\frac{G_a}{100} = 2.2 \,\cdot\,\frac{100}{100} = 2.2</math> | |
| − | |||
| − | |||
| − | + | Für die Soll-Gesamtstärke und Ist-Gesamtstärke des Bogenschützen gilt: | |
| − | |||
| − | |||
| − | + | *<math>\quad B_v - M_v = 0 - 25\, <\, 0 \quad\,\, \Rightarrow \quad\,\, \mathfrak{S}_v = S_v \, \left(1 + \frac{M_v - B_v}{100}\right)^{-1} = 3 \,\cdot\, \left(1 + \frac{25 - 0}{100}\right)^{-1}\, = 3\,\cdot\, \frac{1}{1.25} = 2.4 </math> | |
| − | |||
| − | |||
| − | Gesamtstärke ( | + | * <math> \quad I_v=\mathfrak{S}_v\,\cdot \, \frac{G_v}{100} = 2.4\,\cdot\,\frac{100}{100} = 2.4</math> |
| + | |||
| + | ====Beispiel 2==== | ||
| + | |||
| + | Ein mit ''Kampf I'' (+10% Stärke) beförderter '''Speerkämpfer''' greift einen mit ''Schock'' (+25% gegen Nahkampfeinheiten) beförderten '''Bogenschützen''' auf offenem Gelände an. Beide sind bei voller Gesundheit. | ||
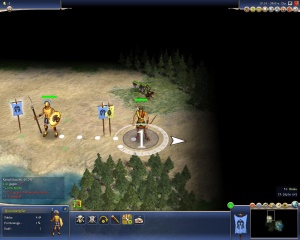
| + | [[Bild:Modi20000.JPG|thumb|Der Bogenschütze erhält durch "Schock" einen Bonus gegen den Speerkämpfer. Da der Bogenschütze verteidigt, kommt der Bonus bei ihm zutragen, anstatt das der Speerkämpfer sanktioniert wird. | ||
| + | Dabei stehen die Zahlen <span style="color:#228B22">'''4.4'''</span> und <span style="color:#ff0000">'''3.75'''</span> für die Ist-Gesamtstärke des Kriegers bzw. des Bogenschützens.]] | ||
| + | Es gilt nun für den '''Speerkämpfer''': | ||
| + | |||
| + | |||
| + | *<math> \quad\mathfrak{S}_a=S_a\, \left( 1 + \frac{B_a}{100} \right) = 4\,\cdot\,\left(1 + \frac{10}{100}\right) = 4.4</math> | ||
| + | |||
| + | |||
| + | *<math> \quad I_a= \mathfrak{S}_a\,\cdot\,\frac{G_a}{100} = 4.4 \,\cdot\,\frac{100}{100} = 4.4</math> | ||
| + | |||
| + | |||
| + | |||
| + | Für '''Bogenschützen''' gilt: | ||
| + | |||
| + | |||
| + | *<math>\quad B_v - M_v = 25 - 0\, >\, 0 \quad\,\, \Rightarrow \quad\,\, \mathfrak{S}_v = S_v \, \left(1 + \frac{B_v - M_v}{100}\right) = 3 \,\cdot\, \left(1 + \frac{25 - 0}{100}\right) = 3.75 </math> | ||
| + | |||
| + | |||
| + | * <math> \quad I_v=\mathfrak{S}_v\,\cdot \, \frac{G_v}{100} = 3.75\,\cdot\,\frac{100}{100} = 3.75</math> | ||
| + | |||
| + | ====Beispiel 3==== | ||
| + | |||
| + | Ein unverletzter Bogenschütze greift einen verletzten Bogenschützen an. Beide sind unbefördert. | ||
| + | |||
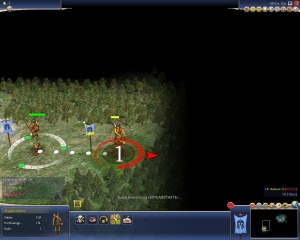
| + | [[Bild:Gesundheit.JPG|thumb|<span style="color:#ff0000">'''49/100 TP'''</span> steht für die aktuelle Gesundheit des Verteidigers. Die Gesundheit des Angreifers beträgt <span style="color:#228B22">'''100/100 TP'''</span>, sie wird aber nicht extra angezeigt. | ||
| + | Dabei stehen die Zahlen <span style="color:#228B22">'''3.00'''</span> und <span style="color:#ff0000">'''1.47'''</span> für die Ist-Gesamtstärke des Kriegers bzw. des Bogenschützens.]] | ||
| + | |||
| + | |||
| + | Für die Soll-Gesamtstärke und Ist-Gesamtstärke des angreifenden Bogenschützen gilt: | ||
| + | |||
| + | |||
| + | *<math> \quad\mathfrak{S}_a=S_a\, \left( 1 + \frac{B_a}{100} \right) = 3\,\cdot\,\left(1 + \frac{0}{100}\right) = 3</math> | ||
| + | |||
| + | |||
| + | *<math> \quad I_a= \mathfrak{S}_a\,\cdot\,\frac{G_a}{100} = 3 \,\cdot\,\frac{100}{100} = 3</math> | ||
| + | |||
| + | |||
| + | Für die Soll-Gesamtstärke und Ist-Gesamtstärke des verteidigenden Bogenschützen gilt: | ||
| + | |||
| + | |||
| + | *<math>\quad B_v - M_v = 0 - 0\, =\, 0 \quad\,\, \Rightarrow \quad\,\, \mathfrak{S}_v = S_v \, \left(1 + \frac{B_v - M_v}{100}\right) = 3 \,\cdot\, \left(1 + \frac{0 - 0}{100}\right)\, = 3 </math> | ||
| + | |||
| + | |||
| + | * <math> \quad I_v=\mathfrak{S}_v\,\cdot \, \frac{G_v}{100} = 3\,\cdot\,\frac{49}{100} = 1.47</math> | ||
=== Feuerkraft (Neu ab Patch 1.61) === | === Feuerkraft (Neu ab Patch 1.61) === | ||
| − | + | '''Definition''' | |
| + | |||
| + | Seien <math>\mathfrak{S}_a,\,\mathfrak{S}_v</math> die ''Soll-Gesamtstärke'' des Angreifers bzw. des Verteidigers unn seien <math>I_a,\,I_v</math> die ''Ist-Gesamtstärke'' des Angreifers und es Verteidigers. | ||
| + | |||
| + | Die '''Feuerkraft''' wird dann definiert als | ||
| + | |||
| + | |||
| + | |||
| + | *Für den Angreifer: <math>\,\,\quad F_a:= floor\left(\frac{I_a + \mathfrak{S}_a}{2}\right) </math> | ||
| + | |||
| + | *Für den Verteidiger:<math>\quad F_v:= floor\left(\frac{I_v + \mathfrak{S}_v}{2}\right) </math> | ||
| + | |||
| + | |||
| + | Dabei bedeutet hier <math> floor(.) </math> das Abrunden auf die 2.Nachkommastelle. | ||
| + | |||
| + | |||
| + | |||
| + | '''Bemerkung''': | ||
| + | |||
| + | Die '''Feuerkraft''' wird mit Hilfe des arithmetischen Mittels aus ''Soll-Gesamtstärke'' und ''Ist-Gesamtstärke'' berechnet. Je kleiner die ''Ist-Gesamtstärke'', desto kleiner ist auch die '''Feuerkraft'''. | ||
| + | |||
| + | ===Angriffwert (Schaden pro Kampfrunde)=== | ||
| + | |||
| + | |||
| + | '''Defintion''' | ||
| − | <math>F_a | + | Seien <math>F_a,\,F_v</math> die ''Feuerkraft'' des Angreifers bzw. des Verteidigers. |
| − | + | Der Angriffwert wird wie folgt definiert: | |
| − | + | *Für den Angreifer:<math>\,\,\quad\mathfrak{A}_a:=floor\left( 20\,\cdot\, \frac{3\,\cdot\,F_a + F_v}{3\,\cdot\,F_v + F_a}\right) </math> | |
| − | + | *Für den Verteidiger:<math>\quad\mathfrak{A}_v:=floor\left( 20\,\cdot\, \frac{3\,\cdot\,F_v + F_a}{3\,\cdot\,F_a + F_v}\right) </math> | |
| + | Dabei bedeutet <math>floor(.)</math> das Abrunden auf die nächstkleinere natürliche Zahl. | ||
| − | ''' | + | '''Bermerkung''' |
| − | + | Der '''Angriffswert''' hängt sowohl von der ''Feuerkraft'' des Angreifers als auch der ''Feuerkraft'' des Verteidigers ab. Dabei gilt: | |
| − | + | ||
| + | *Falls <math>F_a\,>\,F_v</math>, so folgt <math>\,\mathfrak{A}_a\,>\,\mathfrak{A}_v</math>. | ||
| − | + | *Falls <math>F_a\,<\,F_v</math>, so folgt <math>\,\mathfrak{A}_a\,<\,\mathfrak{A}_v</math>. | |
| − | == | + | *Falls <math>F_a\,=\,F_v</math>, so folgt <math>\mathfrak{A}_a\,=\,\mathfrak{A}_v</math>. |
| − | + | ===Anzahl an Trefferpunkten=== | |
| − | + | '''Definition''' | |
| − | <math>\mathfrak{A} | + | Seien <math>G_a,\,G_v</math> die ''Gesundheit'' des Angreifers bzw. des Verteidigers und seien <math>\mathfrak{A}_a,\,\mathfrak{A}_v</math> der ''Angriffwerte' des Angreifers bzw. des Verteidigers. |
| + | Die '''Anzahl an Trefferpunkten''' des Angreifers und des Verteidigers wird wie folgt definiert: | ||
| − | |||
| + | *Für den Angreifer:<math>\,\,\,\quad T_a:=ceil\left(\frac{G_a}{\mathfrak{A}_v}\right) </math> | ||
| − | + | *Für den Verteidiger:<math>\quad T_v:=ceil\left(\frac{G_v}{\mathfrak{A}_a}\right) </math> | |
| − | Für den | ||
| − | |||
| − | |||
| − | + | Dabei bedeutet <math>ceil(.)</math> das Aufrunden auf die nächst größere natürliche Zahl. | |
| − | + | '''Bemerkung''' | |
| − | + | Die '''Anzahl an Trefferpunkte''' des Angreifers hängt von der ''Gesundheit'' des Angreifers und von dem ''Angriffswert'' des Verteidigers ab, die '''Anzahl an Trefferpunkten''' für den Verteidiger hängt von der ''Gesundheit'' des Verteidigers und von dem ''Angriffswert'' des Angreifers ab. | |
| + | Für den Angreifer gilt: Je größer der ''Angriffswert'' des Verteidigers oder die ''Gesundheit'' des Angreifers, desto kleiner ist die '''Anzahl an Trefferpunkten''' des Angreifers. | ||
| − | + | Analog für den Verteidiger. | |
| − | |||
| + | Die '''Anzahl an Trefferpunkten''' ist ein Maß dafür, wieviele Kampfrunden eine Einheit verlieren kann (bzw. wieviele ''Treffer'' sie einstecken kann), bis sie vernichtet ist. | ||
| + | ===Siegrundenwahrscheinlichkeit (die Wahrscheinlichkeit, eine Kampfrunde zu gewinnen)=== | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''Definition''' | |
| + | Seien <math>I_a,\,I_v</math> die ''Ist-Gesamtstärke'' des Angreifers bzw. des Verteidigers. | ||
| − | + | Die '''Siegrundenwahrscheinlichkeit''' ist definiert als: | |
| − | |||
| + | *Für den Angreifer:<math>\,\,\,\quad p_a:= \frac{I_a}{I_a + I_v} </math> | ||
| − | |||
| + | *Für den Verteidiger:<math>\quad p_v:= \frac{I_v}{I_a + I_v} </math> | ||
| + | Es gilt <math> p_a + p_v = 1 </math>. | ||
| − | + | ||
| + | |||
| + | '''Bemerkung''' | ||
| + | |||
| + | Die '''Siegrundenwahrscheinlichkeit''' hängt von der ''Ist-Gesamtgeschwindigkeit'' des Angreifers und des Verteidigers ab. Je größer die ''Ist-Gesamtstärke'' des Angreifers, desto größer ist die '''Siegrundenwahrscheinlichkeit''' des Angreifers und desto kleiner ist die '''Siegrundenwahrscheinlichkeit''' des Verteidigers. | ||
| + | Analog für die ''Ist-Gesamtstärke'' des Verteidigers. | ||
==Berechnung der endgültigen Siegeschance ( ohne Erstschlag)== | ==Berechnung der endgültigen Siegeschance ( ohne Erstschlag)== | ||
| Zeile 217: | Zeile 316: | ||
## <math> G_i - 2\,\cdot\,\mathfrak{A}_j </math> | ## <math> G_i - 2\,\cdot\,\mathfrak{A}_j </math> | ||
## <math> \dots </math> | ## <math> \dots </math> | ||
| − | ## <math> G_i - (R_i-1) | + | ## <math> G_i - (R_i-1) \cdot \mathfrak{A}_j , \text{wobei} \,\, i,j \in \{a, v\}, i \neq j \, .</math> Dies bedeutet, <math> i </math> und <math>j</math> können für den Angreifer oder den Verteidiger stehen, wobei sie voneinander verschieden sind. (Kleines Beispiel: Angenommen, ein Angreifer mit voller Gesundheit gewinne einen Kampf und der Verteidiger habe einen Angriffswert <math>\mathfrak{A}_v = 17 </math>. Dann kommen für den Angreifer folgende Kampfausgänge in betracht: [[Bild:Gesundheit Angreifer.jpg|thumb|Die Grafik gibt die verschiedenen Kampfausgänge des hier gemachten Beispieles an unter der Voraussetzung, dass der Angreifer den Kampf gewinnt und das der Verteidiger einen Angriffswert von 17 besitzt. Die einzelnen Balkenhöhen stellen die Wahrscheinlichkeiten dafür dar, mit welchem Zustand der Angreifer gewinnt. "100" steht für volle Gesundheit, "15" steht hier für "fast am Ende".]]. |
###100 Gesundheit | ###100 Gesundheit | ||
###83 Gesundheit | ###83 Gesundheit | ||
| Zeile 224: | Zeile 323: | ||
###32 Gesundheit | ###32 Gesundheit | ||
###15 Gesundheit | ###15 Gesundheit | ||
| − | ### 0 oder weniger Gesundheit ist nicht möglich, andernfalls wäre der Angreifer besiegt, was aber der Voraussetzung, dass er den Kampf gewonnen hat, widerspricht.) | + | ### 0 oder weniger Gesundheit ist nicht möglich, andernfalls wäre der Angreifer besiegt, was aber der Voraussetzung, dass er den Kampf gewonnen hat, widerspricht.) |
| + | |||
#Die in 3. eintretenden Kampfausgänge besitzen unterschiedliche Wahrscheinlichkeiten, aus denen sich dann hinterher die Siegeswahrscheinlichkeit zusammensetzt. | #Die in 3. eintretenden Kampfausgänge besitzen unterschiedliche Wahrscheinlichkeiten, aus denen sich dann hinterher die Siegeswahrscheinlichkeit zusammensetzt. | ||
| − | #Diese Wahrscheinlichkeiten werden durch die sogenannte Binominalverteilung ermittelt. | + | #Diese Wahrscheinlichkeiten werden durch die sogenannte Binominalverteilung ermittelt. |
| − | |||
=== Die Binominalverteilung === | === Die Binominalverteilung === | ||
| Zeile 233: | Zeile 332: | ||
Betrachten wir dazu das Modell des fortgesetzten Münzwurf. | Betrachten wir dazu das Modell des fortgesetzten Münzwurf. | ||
| − | Eine Münze wird 5-mal geworfen. Wie groß ist die Wahrscheinlichkeit, dass 3-mal die Zahl | + | Eine Münze wird 5-mal geworfen. Wie groß ist die Wahrscheinlichkeit, dass 3-mal die Zahl fällt? |
| − | Den 5-maligen Wurf der Münze können wir als eine Null-Eins-Folge interpretieren, wobei die Eins für das Ereignis steht, dass die Zahl | + | Den 5-maligen Wurf der Münze können wir als eine Null-Eins-Folge interpretieren, wobei die Eins für das Ereignis steht, dass die Zahl fällt, die Null steht dann entsprechend für das Ereignis, dass Kopf fällt. Eine mögliche günstige Kette wäre dann z.B. 1-0-1-1-0. |
| − | + | Die Reihenfolge der Ereignisse ist egal, wichtig ist nur, wieoft die Eins oder die Null kommt. | |
| − | |||
| − | |||
| − | + | Die Wahrscheinlichkeit, mit der aus dem 5-maligen Werfen 3-mal die Eins kommt, beträgt <math>{5\choose 3}\,\cdot\, 0.5^3\,\cdot\,0.5^2 = 0.31250 </math>, wobei <math>{5\choose 3} = \frac{5!}{3!\,(5-3)!}</math> der Binominalkoeffizient ist. | |
| − | + | ||
| − | + | Sei ''n'' die Länge einer Null-Eins-Folge. Die Wahrscheinlichkeit, mit der die Folge ''k''-Einsen enthält, beträgt | |
| + | |||
| + | <math>B(n,p,k)= {n\choose k}\,\cdot\,p^k\,\cdot\,(1-p)^{n-k} </math>, wobei ''p'' die Wahrscheinlichkeit dafür ist, mit der eine Eins fällt. | ||
| + | |||
| + | ''B(n,p,k)'' bezeichnet man dann als '''Binominalverteilung'''. | ||
=== Formel für die Berechnung der Siegeswahrscheinlichkeit === | === Formel für die Berechnung der Siegeswahrscheinlichkeit === | ||
| + | Betrachten wir einen Kampf, bei dem der Angreifer gewinnt. Wie weiter oben beschrieben, können mehrere Ausgänge eintreten, was den Grad der Verletzung des Angreifers betrifft. | ||
| + | Im Folgenden betrachten wir uns den Ausgang, dass der Angreifer unverletzt aus dem Kampf hervor geht. Das bedeutet, der Angreifer darf keine Kampfrunden verlieren, andernfalls würde er verletzt werden, was wir aber erstmal ausschließen. | ||
| − | + | Führen wir erstmal folgende Definition ein: | |
| − | |||
| − | |||
| − | + | '''Definition''' | |
| − | + | Seien <math>T_a</math> und <math>T_v</math> die ''Anzahl an Trefferpunkten'' des Angreifers bzw. des Verteidigers. | |
| − | |||
| − | |||
| − | + | Die '''maximale Anzahl an Kampfrunden''' ergibt sich dann wie folgt: | |
| − | |||
| − | |||
| − | |||
| + | *<math> R_{max}:= T_a + T_v - 1 </math> | ||
| − | |||
| − | + | (-1 deswegen, weil Angreifer und Verteidiger beide gleichzeitig den Kampf nicht verlieren können.) | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Als Null-Eins-Folge interpretiert gilt: 1-1-1-...-1 , wobei die Eins dafür steht, dass der Angreifer die Kampfrunde gewinnt. Die Anzahl der Einser ist im diesem Falle gleich den Wert von <math>R_v</math>. | ||
| + | Die Binominalverteilung darauf angewandt ergibt: | ||
| − | + | <math>B(T_v\,,\,p_a\,,\,T_v)= {T_v\choose T_v}\,\cdot\,{p_a}^{T_v}\,\cdot\,{p_v}^{T_v-T_v} = {T_a}^{T_v} </math> | |
| − | |||
| − | + | Dies ist die Wahrscheinlichkeit dafür, dass der Angreifer unverletzt den Kampf gewinnt. | |
| − | |||
| − | + | Wird der Angreifer einmal getroffen, also er verliert genau eine Kampfrunde, dann gilt: | |
| − | + | <math>B(T_v\,,\,p_a\,,\,T_v-1)\,\cdot\,p_a = {T_v\choose T_v-1}\,\cdot\,{p_a}^{T_v-1}\,\cdot\,p_a\,\cdot\,{p_v}^{T_v-(T_v-1)} = {T_v\choose T_v-1}\,\cdot\,{p_a}^{T_v}\,\cdot\,{p_v}</math> | |
| + | |||
| + | |||
| + | Warum <math> B(T_v\,,\,p\,,\,T_v-1)\,\cdot\,p </math> und nicht <math> B(T_v+1\,,\,p_a\,,\,T_v)</math> ? | ||
| + | Hierzu betrachten wir uns die dazu gehörende Null-Eins-Folge: 1-1-...-0-...-1-1 . Die Folge enthält genau eine Null. Diese kann an einer beliebigen Stelle aufhalten, außer an der letzten. Die letzte Eins steht dafür, dass der Angreifer den letzten Treffer gegen den Verteidiger landet und ihn somit besiegt. Würde aber am Ende die einzige Null stehen, würde dass heißen, dass der Kampf nicht zu Ende wäre. Somit muss die letzte Stelle von einer Eins belegt sein. Als Konsequenz reduzieren sich automatisch die möglichen günstigen Anordnungen der Null-Eins-Folge. | ||
| + | (Zusammengefasst muss der letzte Treffer immer vom Angreifer kommen, wenn er siegen will.) | ||
| + | |||
| + | Wird der Angreifer zweimal getroffen, so gilt entsprechend: | ||
| + | |||
| + | <math>B(T_v+1\,,\,p_a\,,\,T_v-1)\,\cdot\,p_a = {T_v+1\choose T_v-1}\,\cdot\,{p_a}^{T_v-1}\,\cdot\,p_a\,\cdot\,{p_v}^{T_v+1-(T_v-1)} = {T_v+1\choose T_v-1}\,\cdot\,{p_a}^{T_v}\,\cdot\,{p_v}^2 </math> | ||
| − | |||
| + | Allgemein gilt nun für die Wahrscheinlichkeit, dass der Angreifer den Kampf gewinnt: | ||
| − | = | + | <math>B(T_v\,,\,p_a\,,\,T_v) + \sum_{n=T_v}^{R_{max}-1} B(n\,,\,p_a,T_v)\,\cdot\,p_a </math> |
| − | |||
| − | |||
| − | + | Der erste Summand ist gerade die Wahrscheinlichkeit, dass der Angreifer unverletzt den Kampf gewinnt, er also keine Kampfrunde verliert. Der zweite Summand steht dafür, dass der Angreifer genau eine Kampfunde verliert. Der letzte Summand steht dafür, dass der Angreifer <math>(T_a - 1)</math> Kampfrunden verliert, das bedeutet, dass er fast am Ende ist, eine weitere verlorene Runde würde einen Niederlage bedeuten. (<math>T_a - 1</math> taucht nicht direkt in der Formel auf, es steht aber für die Anzahl aller Summanden.) | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''Definition''': | |
| − | + | Seien <math>T_a\,,\,T_v\,\in\mathbb{N}</math> die ''Anzahl an Trefferpunkten'' des Angreifers bzw. des Verteidigers und seien <math>p_a\,,\,p_v\,\in\,[0,1]</math> die Wahrscheinlichkeiten dafür, dass der Angreifer bzw. der Verteidiger eine Kampfrunde gewinnt mit <math>p_a + p_v = 1</math>. | |
| + | Dann gilt | ||
| − | == | + | *<math> P_a:= B(T_v\,,\,p_a\,,\,T_v) + \sum_{n=T_v}^{R_{max}-1} B(n\,,\,p_a\,,\,T_v)\,\cdot\,p_a </math> und |
| + | *<math> P_v:= B(T_a\,,\,p_v\,,\,T_a) + \sum_{n=T_a}^{R_{max}-1} B(n\,,\,p_v\,,\,T_a)\,\cdot\,p_v </math>, | ||
| − | |||
| − | + | wobei <math>P_a</math> für die Siegeswahrscheinlichkeit des Angreifers steht, den Kampf zu gewinnen, <math>P_v</math> steht entsprechend für die Wahrscheinlichkeit eines Sieges des Verteidigers. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ( | + | ==Berechnung der endgültigen Siegeschance ( mit Erstschlag)== |
| − | |||
| − | |||
| − | + | ===Erstschläge=== | |
| − | |||
| − | |||
| − | + | Als Erstschläge werden Kampfrunden bezeichnet, in denen eine Einheit, die Erstschläge zur Verfügung hat, nicht verletzt werden kann. Ansonsten sind sie mit den normalen Kampfrunden identisch. Allgemein gelten folgende Rahmenbedingungen für den Einsatz von Erstschlägen: | |
| − | |||
| − | |||
| − | |||
| − | + | *Eine Einheit kann nur über Erstschläge verfügen, wenn sie mit entsprechenden Beförderungen (Erschlag I-V) ausgestattet wird oder sie bereits als Einheitenfähigkeit besitzt (z.B. besitzt der Bogenschütze einen Erstschlag). | |
| − | + | *Besitzt eine Einheit Erstschläge, so hat sie eine gewisse Anzahl an "freien" Kampfrunden, in denen sie zwar wie gewohnt ihren Gegner verletzten kann, ohne aber dabei selber befürchten zu müssen, verletzt zu werden. | |
| + | *Die Anzahl der "freien" Kampfrunden ist der Betrag aus der Differenz der Anzahl an Erstschlägen des Angreifers und der Anzahl an Erstschlägen des Verteidigers. | ||
| + | *"Freie" Kampfrunden kann nur entweder der Angreifer haben oder der Verteidiger, beide können nicht gleichzeitig während eines Kampfes "freie" Kampfrunden haben. Es ist auch möglich, dass es in einem Kampf keine "freie" Kampfrunden vorkommen. Dies ist genau dann der Fall, wenn Angreifer und Verteidiger die gleiche Anzahl an Erstschlägen besitzten. | ||
| + | *Es gibt Einheiten, die immun gegen Erstschläge sind, sei es durch Einheiteneigenschaft oder durch bestimmte Beförderungen. Auch in diesem Fall gibt es keine Kampfrunden. | ||
| + | *Erstschläge laufen vor dem eigentlichen Kampf ab. Theoretisch könnte bei einer ausreichend hohen Anzahl an verfügbaren Erstschlägen der Kampf gewonnen werden, ohne dass der Feind die Möglichkeit zur Gegenwehr hätte (was aber in der Praxis ein unwahrscheinlicher Fall ist). | ||
| − | |||
| − | + | Sei nun <math>e:= \|E_a - E_v \|</math> der Betrag von der Differenz aus den verfügbaren Erstschlägen des Angreifers und Verteidigers. | |
| + | Weiterhin gilt: | ||
| − | + | 1) Falls <math>E_a - E_v \,>\, 0 \Rightarrow</math> der Angreifer verfügt über <math>e</math>-Erstschläge | |
| − | + | 2) Falls <math>E_a - E_v \,<\, 0 \Rightarrow</math> der Verteidiger verfügt über <math>e</math>-Erstschläge | |
| − | + | 3) Falls <math>E_a - E_v \,=\, 0 \Rightarrow</math> Angreifer und Verteidiger verfügen über 0-Erstschläge | |
| − | + | ===Endgültige Berechnung=== | |
| − | |||
| − | + | Seien mit <math>R_a\,,\,R_v\,\in\mathbb{N}</math> die Runde gemeint, mit der der Angreifer bzw. der Verteidiger den Kampf verliert und seien <math>p_a\,,\,p_v\,\in\,[0,1]</math> die Wahrscheinlichkeiten dafür, dass der Angreifer bzw. der Verteidiger den Kampf gewinnen, <math>p_a + p_v = 1</math>, <math>e\,\in\mathbb{N}_0</math> sei die Anzahl der im Kampf eingesetzten Erstschläge. | |
| − | + | Falls 1) zutrifft, dann gilt: | |
| − | B ( | + | *<math>P_a(i):= B(R_v-i\,,\,p_a\,,\,R_v-i)\, + \,\sum_{n=k}^{m} B(n\,,\,p_a\,,\,R_v-1-i)\,\cdot\,p_a\,,\quad k:= R_v-1\,,\quad m:= R_{max}-1-i</math> |
| + | *<math>P_v(i):= B(R_a\,,\,p_v\,,\,R_a)\,+\,\sum_{n=R_a}^{m} B(n\,,\,p_v\,,\,R_a-1)\,\cdot\,p_v\,,\quad m:= R_{max}-1-i </math> | ||
| − | |||
| − | + | Falls 2) zutrifft, dann gilt: | |
| − | + | *<math>P_a(i):= B(R_v\,,\,p_a\,,\,R_v)\,+\,\sum_{n=R_v}^{m} B(n\,,\,p_a\,,\,R_v-1)\,\cdot\,p_a\,,\quad m:= R_{max}-1-i</math> | |
| − | + | *<math>P_v(i):= B(R_a-i\,,\,p_v\,,\,R_a-i)\,+\,\sum_{n=k}^{m} B(n\,,\,p_v\,,\,R_a-1-i)\,\cdot\,p_v\,,\quad k:= R_a-1\,,\quad m:= R_{max}-1-i </math> | |
| − | |||
| − | |||
| − | + | Falls 3) zutrifft, dann gilt: | |
| − | + | *<math> P_a(0):= B(R_v\,,\,p_a\,,\,R_v)\,+\,\sum_{n=R_v}^{R_{max}-1} B(n\,,\,p_a\,,\,R_v)\,\cdot\,p_a </math> | |
| − | B( | + | *<math> P_v(0):= B(R_a\,,\,p_v\,,\,R_a)\,+\,\sum_{n=R_a}^{R_{max}-1} B(n\,,\,p_v\,,\,R_a)\,\cdot\,p_v </math> |
| − | B( | ||
| − | B( | ||
| − | B( | ||
| − | |||
| − | + | wobei <math>0\leq i \leq e</math>, <math>P_a(i)</math> steht für die Wahrscheinlichkeit des Angreifers, beim <math>i</math>-ten Erstschlag den Kampf zu gewinnen, <math>P_v(i)</math> steht für die Wahrscheinlichkeit des Verteidigers, beim <math>i</math>-ten Erstschlag den Kampf zu gewinnen. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Weiterhin gilt: | |
| − | + | *<math>PG_a:= \sum_{k=0}{e} P_a(k)\,\cdot\,B(e\,,\,0.5\,,\,k)</math> | |
| − | + | *<math>PG_v:= \sum_{k=0}{e} P_v(k)\,\cdot\,B(e\,,\,0.5\,,\,k)</math> | |
| − | + | wobei <math>PG_a,\,PG_v</math> für die Siegeswahrscheinlichkeiten des Angreifers bzw. des Verteidigers stehen. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Zur Erläuterung der obigen Formeln befassen wir uns nur mit Fall (1). (Fall (2) geht vom Prinzip her analog, Fall (3) hatten wir schon weiter oben behandelt.) | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Als Beispiel wählen wir <math>e=2</math>. Dann gilt für den Angreifer: | |
| − | 1 | + | <math>P_a(0):= B(R_v-0\,,\,p_a\,,\,R_v-0)\, + \,\sum_{n=k}^{m} B(n\,,\,p_a\,,\,R_v-1-0)\,\cdot\,p_a\,,\quad k:= R_v-1\,,\quad m:= R_{max}-1-0</math> |
| − | + | <math>P_a(1):= B(R_v-1\,,\,p_a\,,\,R_v-1)\, + \,\sum_{n=k}^{m} B(n\,,\,p_a\,,\,R_v-1-1)\,\cdot\,p_a\,,\quad k:= R_v-1\,,\quad m:= R_{max}-1-1</math> | |
| − | B ( | ||
| − | |||
| − | B ( | ||
| − | |||
| − | |||
| − | + | <math>P_a(2):= B(R_v-2\,,\,p_a\,,\,R_v-2)\, + \,\sum_{n=k}^{m} B(n\,,\,p_a\,,\,R_v-1-2)\,\cdot\,p_a\,,\quad k:= R_v-1\,,\quad m:= R_{max}-1-2</math> | |
| − | |||
| − | + | <math>PG_a = \sum_{k=0}^2 P_a(k)\,\cdot\,B(2\,,\,0.5\,,\,k)</math> | |
| − | |||
| − | B ( | ||
| − | |||
| − | |||
| − | |||
| − | + | Für den Verteidiger gilt: | |
| − | + | <math>P_v(0):= B(R_a\,,\,p_v\,,\,R_a)\,+\,\sum_{n=R_a}^{m} B(n\,,\,p_v\,,\,R_a-1)\,\cdot\,p_v\,,\quad m:= R_{max}-1-0 </math> | |
| − | |||
| − | |||
| − | + | <math>P_v(1):= B(R_a\,,\,p_v\,,\,R_a)\,+\,\sum_{n=R_a}^{m} B(n\,,\,p_v\,,\,R_a-1)\,\cdot\,p_v\,,\quad m:= R_{max}-1-1 </math> | |
| − | + | <math>P_v(2):= B(R_a\,,\,p_v\,,\,R_a)\,+\,\sum_{n=R_a}^{m} B(n\,,\,p_v\,,\,R_a-1)\,\cdot\,p_v\,,\quad m:= R_{max}-1-2 </math> | |
| − | + | <math>PG_v = \sum_{k=0}^2 P_v(k)\,\cdot\,B(2\,,\,0.5\,,\,k)</math> | |
| − | |||
| − | + | ==Beispielrechnung== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | ==Zusätzliches== | ||
| − | |||
| − | |||
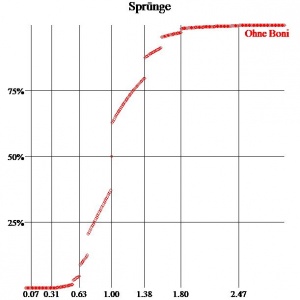
| − | + | [[Bild:Sprünge.jpg|thumb|Die Grafik stellt die Siegeswahrscheinlichkeit in Abhängigkeit vom Stärkequotienten zwischen Angreifer und Verteidiger dar. Die horizontale Achse steht für den Stärkequotienten (von 0 bis 3), die vertikale für die Siegeswahrscheinlickeiten (von 0% bis 100%. Bei einem Stärkequotienten von 1 beträgt die Siegeswahrscheinlichkeit des Angreifers genau 50%, ist der Quotient kleiner als 1 (größer als 1), so ist, die Siegeswahrscheinlichkeit für den Angreifer kleiner (bzw. größer) als 50%.]] | |
Aktuelle Version vom 13. April 2013, 01:34 Uhr
| |
Dieser Artikel erläutert das Kampfsystem in Civilization IV. Für das gleichnamige Spielkonzept in anderen Teilen der Civilization-Reihe siehe Kampfsystem. |
Inhaltsverzeichnis
- 1 Einführung
- 2 Vorberechnungen
- 3 Berechnung der endgültigen Siegeschance ( ohne Erstschlag)
- 4 Berechnung der endgültigen Siegeschance ( mit Erstschlag)
- 5 Beispielrechnung
- 6 Zusätzliches
Einführung
In diesem Artikel wird das Kampfsystem von Civilisation 4 erläutert. Der Artikel wird Schrittweise auf die einzelnen Berechnungen eingehen. Ziel des Artikels ist dazustellen, wie sich die Wahrscheinlichkeit, mit der eine Einheit eine andere besiegt, berechnen lässt.
In den Nachfolgenden Abschnitten wird Grundsätzliches zum Kampfverlauf geschildert und es wird auf die einen Teil der Notation eingegangen. Immer, wenn neue Begriffe auftauchen, wird gleich die Schreibweise mit benannt. So wird nicht zuviele Symbole auf einmal auf einen einstürmen.
Im 2.Teil werden die ganzen Vorberechnungen erläutert, die für die Hauptberechnungen im 3.Teil unerlässlich sind. Es werden folgende Begriffe eingeführt, erläutert und mit Beispielen untermauert:
- Ist-Gesamtstärke und Soll-Gesamtstärke
- Feuerkraft
- Schaden pro Runde oder der Angriffswert
- Anzahl an Kampfrunden, die eine Einheit verlieren kann, eher sie besiegt ist
- Wahrscheinlichkeit, eine Kampfrunde zu gewinnen bzw. zu verlieren
Im 3.Teil kommen wir zu den eigentlichen Hauptberechnungen. Zentrales Hilfsmittel ist die sogenannte Binominalverteilung. Sie wird kurz umrissen werden. Es wird dann gezeigt, wie sich die Wahrscheinlichkeit, mit der ein Kampf gewonnen wird, berechnen lässt, ohne auf das Konzept der Erstschläge einzugehen. Auch hier wird es wieder eine Beispielrechnung geben. Anschließend wird dann auf das Konzept der Erstschläge eingegangen. Es wird erläutert, was Erstschläge überhaupt sind, was sie bewirken und welchen Einfluss sie auf die Berechnungen der Siegwahrscheinlichkeit ausüben. (Es sei angemerkt, dass sich durch die Erstschläge die Berechnungen "etwas" komplizierter werden, allerdings in einem noch erträglichem Maße.)
Allgemeines
Zuerst soll hier erstmal die genauen Rahmenbedingungen erklärt werden, d.h. wie ein Kampf in Civ4 überhaupt abläuft:
- An einem Kampf sind genau zwei Einheiten beteiligt: der Angreifer und der Verteidiger.
- Als Angreifer wird diejenige Einheit angesehen, die selbst ein benachtbartes Feld betritt, in der sich eine andere, feindliche Einheit aufhält, diese wird dann als Verteidiger bezeichnet.
- Festlegung auf Angreifer und Verteidiger hat nur Einfluss darauf, wer welche Art von Boni bzw. Mali bekommen kann. Der Verteidiger z.B. bekommt immer Boni durch das Gelände (falls vorhanden), in dem er sich zum Zeitpunkt des Angriffs befindet. Der Angreifer bekommt solche Boni nie. Außerdem gibt es noch ein paar Besonderheiten derart, wer welche Art von Boni bzw. Mali bekommt. Darauf wird weiter unten eingegangen.
- Als Ausgänge eines Kampfes kommen nur ein Sieg des Angreifers oder ein Sieg des Verteidigers in Betracht. Falls der Angreifer den Kampf verliert, kann er sich noch unter gewissen Umständen aus dem Kampf zurückziehen. Auch darauf wird weiter unten eingegangen.
- Gewinnt eine Einheit einen Kampf (egal ob Angreifer oder Verteidiger), so wird er in den meisten Fällen verletzt aus dem Kampf gehen. Jede Einheit besitzt nach ihrer Errichtung volle 100 Trefferpunkte (Abkürzung Tp). Eine Einheit gilt als vernichtet, wenn sie genau 0 Tp besitzt. Dies tritt nur nach einer Niederlage in einem Kampf auf. Eine Einheit kann sich nach dem Kampf von ihren Verletzungen erholen.
- Ein Kampf läuft in einzelnen Runden ab (nicht zu verwechseln mit einer normalen Civ4 Runde!). Eine Kampfrunde wird entweder von dem Angreifer gewonnen oder von dem Verteidiger, ein Unentschieden ist nicht möglich. Gewinnt der Angreifer eine Runde, so erhält der Verteidiger einen Treffer, seine Gesundheit verringert sich dem entsprechend dem Angriffswert des Angreifers (mit Angriffswert ist nicht die Stärke gemeint! Siehe weiter unten). Gewinnt der Verteidiger, so gilt entsprechendes für den Angreifer.
- Ein Kampf gilt genau dann als beendet, wenn entweder der Angreifer oder der Verteidiger nur noch 0 Tp besitzten. Diese Einheit gilt als vernichtet und wird vom Spiel entfernt. Einzige Ausnahme betrifft die bereits angesprochene Rückzugsmöglichkeit des Angreifers. Dieser Fall tritt dann ein, wenn der Angreifer fast erledigt ist und somit ein letzter Treffer des Verteidigers ihn vernichten würde. Würde dann der Verteidiger diese Kampfrunde gewinnen, so zieht sich der Angreifer zurück, ohne den Treffer einzustecken.
- Eine verringerte Gesundheit hat direkte Auswirkung auf die Stärke einer Einheit. Ist eine Einheit schwer verletzt, ist sie kaum noch kampffähig. Auf diese Weise ist es möglich, eigentlich sehr starke Einheiten wie z.B. einen Panzer mit einer verhältnismäßigen schwachen Einheit (z.B. ein Speerkämpfer) zu besiegen.
- Die Stärke einer Einheit ändert sich während eines Kampfes nicht, auch nicht, sollte er verletzt werden. Verletzungen machen sich erst beim nächsten Kampf bemerkbar.
- Boni können die Kampfkraft einer Einheit deutlich erhöhen, durch Mali kann sie aber auch deutlich verringert werden.
- Eine Einheit kann befördert werden. Die meisten Beförderungen geben Boni auf bestimmte Kampfbedingungen, z.B. gibt die Beförderung Schock einer Einheit einen +25% Bonus gegen Nahkampeinheiten.
Vorberechnungen
Kampfmodifikatoren
Einheiten können mit bestimmten Beförderungen ihre Kampfkraft verbessern. Auch spielt das Gelände, wo der Kampf ausgetragen wird, eine große Rolle. Nachfolgend werden alle Modifikatoren aufgelistet, die den Kampf beeinflussen (jeweils für den Angreifer und für den Verteidiger):
Modifikatoren, die auf den Angreifer wirken
- Kampf I-VI
Modifikatoren, die auf den Verteidiger wirken
- Kampf I-VI
- Angriff, Deckung, Finte, Formation, Hinterhalt, Schock
- Häuserkampf I-III
- Garnison I-III
- Guerilla I-III, Waldkampf I-III
- Speerfeuer II-III
- Gelände: Hügel, Wald, Fluss (falls Angreifer ohne Beförderung Amphibisch), Amphibische Landung (falls Angreifer ohne Beförderung Amphibisch)
- Verschanzung und Kulturverteidigung
- Diverse Einheitenfähigkeiten
Im folgendem steht für die Boni, die der Angreifer bekommt, und steht für die Boni bzw. Mali, die der Verteidiger bekommt. Der Angreifer selbst wird niemals Mali bekommen.
(Beispiele hierfür im nächsten Abschnitt.)
Berechnung von Ist-Gesamtstärke und Soll-Gesamtstärke
Definition
Seien die Sollstärke des Angreifers bzw. des Verteidigers, seien die Boni des Angreifers bzw. des Verteidigers, sei die Mali des Verteidigers, seinen die Gesundheitwerte des Angreifers bzw. des Verteidigers.
Dann werden Soll-Gesamtstärke und Ist-Gesamtstärke des Angreifers bzw. des Verteidigers wie folgt berechnet:
- Für den Angreifer:
- Für den Verteidiger:
- Für den Angreifer:
- Für den Verteidiger:
Bemerkung:
Mit Sollstärke ist die Stärke gemeint, die eine Einheit bei ihrer Errichtung besitzt. Zum Beispiel besitzt ein Bogenschütze eine Sollstärke von 3. (Anders ausgedrückt ist mit Sollstärke die Stärke gemeint, die eine Einheit bei voller Gesundheit besitzt.) Die Sollstärke ist immer eine natürliche Zahl, die Null ist nicht dabei (deswegen auch die Schreibweise ). (Zur Erinnerung: Natürliche Zahlen sind: )
Die Boni und Mali nehmen ebenfalls nur Werte aus den nathürlichen Zahlen an, diesmal aber mit der Null (deswegen auch die Schreibweise ).
Die Gesundheit nimmt Werte aus den natürlichen Zahlen von 1 bis 100 an (deswegen die Schreibweise ). Ein Wert von 100 bedeutet volle Gesundheit einer Einheit, und dadurch bedingt auch volle Stärke. Ein Wert von 0 bedeutet, dass die Einheit vernichtet ist. (Vernichtete Einheiten können nicht mehr kämpfen, deswegen wird hier der Wert 0 als Gesundheitswert nicht zugelassen.)
Die Soll-Gesamtstärke des Angreifers hängt von der Sollstärke des Angreifers und von dessen Boni ab. Je größer die Sollstärke oder die Boni sind, desto größer ist die Soll-Gesamtstärke.
Sind keine Boni vorhanden, dann entspricht die Soll-Gesamtstärke gerade der Sollstärke.
Für den Verteidiger gilt das gleiche, nur kommen noch die Mali dazu.
Es müssen hier 2 Fälle unterschieden werden. Ist die Differenz aus Boni und Mali positiv, so wird die Sollstärke mit der Klammer (aus der Formel oben) multipliziert. Ist die Differenz negativ, so wird die Sollstärke durch die Klammer dividiert.
Je größer also die Mali, desto kleiner die Soll-Gesamtstärke.
Die Ist-Gesamtstärke unterscheidet sich von der Soll-Gesamtstärke nur derart, dass nun auch die Gesundheit ein Parameter ist. Ist der Wert der Gesundheit gleich 100, so entspricht die Ist-Gesamtstärke gerade der Soll-Gesamtstärke. Je geringer die Gesundheit ist, desto geringer ist auch die Ist-Gesamtstärke.
Beispiel 1
Ein unverletzter Krieger mit den Beförderungen Kampf I (+10% Stärke) und Deckung (+25% gegen Bogenschützen) will einen ebenfalls unverletzten, aber unbeförderten Bogenschützen auf offenem Gelände angreifen.
Für die Soll-Gesamtstärke und Ist-Gesamtstärke des Kriegers gilt:
Für die Soll-Gesamtstärke und Ist-Gesamtstärke des Bogenschützen gilt:
Beispiel 2
Ein mit Kampf I (+10% Stärke) beförderter Speerkämpfer greift einen mit Schock (+25% gegen Nahkampfeinheiten) beförderten Bogenschützen auf offenem Gelände an. Beide sind bei voller Gesundheit.
Es gilt nun für den Speerkämpfer:
Für Bogenschützen gilt:
Beispiel 3
Ein unverletzter Bogenschütze greift einen verletzten Bogenschützen an. Beide sind unbefördert.
Für die Soll-Gesamtstärke und Ist-Gesamtstärke des angreifenden Bogenschützen gilt:
Für die Soll-Gesamtstärke und Ist-Gesamtstärke des verteidigenden Bogenschützen gilt:
Feuerkraft (Neu ab Patch 1.61)
Definition
Seien die Soll-Gesamtstärke des Angreifers bzw. des Verteidigers unn seien die Ist-Gesamtstärke des Angreifers und es Verteidigers.
Die Feuerkraft wird dann definiert als
- Für den Angreifer:
- Für den Verteidiger:
Dabei bedeutet hier das Abrunden auf die 2.Nachkommastelle.
Bemerkung:
Die Feuerkraft wird mit Hilfe des arithmetischen Mittels aus Soll-Gesamtstärke und Ist-Gesamtstärke berechnet. Je kleiner die Ist-Gesamtstärke, desto kleiner ist auch die Feuerkraft.
Angriffwert (Schaden pro Kampfrunde)
Defintion
Seien die Feuerkraft des Angreifers bzw. des Verteidigers.
Der Angriffwert wird wie folgt definiert:
- Für den Angreifer:
- Für den Verteidiger:
Dabei bedeutet das Abrunden auf die nächstkleinere natürliche Zahl.
Bermerkung
Der Angriffswert hängt sowohl von der Feuerkraft des Angreifers als auch der Feuerkraft des Verteidigers ab. Dabei gilt:
- Falls , so folgt .
- Falls , so folgt .
- Falls , so folgt .
Anzahl an Trefferpunkten
Definition
Seien die Gesundheit des Angreifers bzw. des Verteidigers und seien der Angriffwerte' des Angreifers bzw. des Verteidigers.
Die Anzahl an Trefferpunkten des Angreifers und des Verteidigers wird wie folgt definiert:
- Für den Angreifer:
- Für den Verteidiger:
Dabei bedeutet das Aufrunden auf die nächst größere natürliche Zahl.
Bemerkung
Die Anzahl an Trefferpunkte des Angreifers hängt von der Gesundheit des Angreifers und von dem Angriffswert des Verteidigers ab, die Anzahl an Trefferpunkten für den Verteidiger hängt von der Gesundheit des Verteidigers und von dem Angriffswert des Angreifers ab.
Für den Angreifer gilt: Je größer der Angriffswert des Verteidigers oder die Gesundheit des Angreifers, desto kleiner ist die Anzahl an Trefferpunkten des Angreifers.
Analog für den Verteidiger.
Die Anzahl an Trefferpunkten ist ein Maß dafür, wieviele Kampfrunden eine Einheit verlieren kann (bzw. wieviele Treffer sie einstecken kann), bis sie vernichtet ist.
Siegrundenwahrscheinlichkeit (die Wahrscheinlichkeit, eine Kampfrunde zu gewinnen)
Definition
Seien die Ist-Gesamtstärke des Angreifers bzw. des Verteidigers.
Die Siegrundenwahrscheinlichkeit ist definiert als:
- Für den Angreifer:
- Für den Verteidiger:
Es gilt .
Bemerkung
Die Siegrundenwahrscheinlichkeit hängt von der Ist-Gesamtgeschwindigkeit des Angreifers und des Verteidigers ab. Je größer die Ist-Gesamtstärke des Angreifers, desto größer ist die Siegrundenwahrscheinlichkeit des Angreifers und desto kleiner ist die Siegrundenwahrscheinlichkeit des Verteidigers. Analog für die Ist-Gesamtstärke des Verteidigers.
Berechnung der endgültigen Siegeschance ( ohne Erstschlag)
Allgemeines
Jetzt kommen wir zud den eigentlichen Berechnungen, die die Wahrscheinlichkeit wiedergibt, einen Kampf zu gewinnen. Dazu erstmal ein paar weitere allgemeine Sachen:
- Ein Kampf hat genau zwei Ausgänge. Entweder siegt der Angreifer oder der Verteidiger.
- Die siegreich aus dem Kampf kommende Einheit wird eine Restgesundheit übrig haben, die im Bereich zwischen 1 und derjenigen Gesundheit liegt, mit der gekämpft wurde.
- Für die siegreiche Einheit können folgende Kampfausgänge eintreten:
- Dies bedeutet, und können für den Angreifer oder den Verteidiger stehen, wobei sie voneinander verschieden sind. (Kleines Beispiel: Angenommen, ein Angreifer mit voller Gesundheit gewinne einen Kampf und der Verteidiger habe einen Angriffswert . Dann kommen für den Angreifer folgende Kampfausgänge in betracht: .
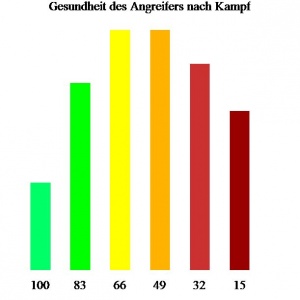 Die Grafik gibt die verschiedenen Kampfausgänge des hier gemachten Beispieles an unter der Voraussetzung, dass der Angreifer den Kampf gewinnt und das der Verteidiger einen Angriffswert von 17 besitzt. Die einzelnen Balkenhöhen stellen die Wahrscheinlichkeiten dafür dar, mit welchem Zustand der Angreifer gewinnt. "100" steht für volle Gesundheit, "15" steht hier für "fast am Ende".
Die Grafik gibt die verschiedenen Kampfausgänge des hier gemachten Beispieles an unter der Voraussetzung, dass der Angreifer den Kampf gewinnt und das der Verteidiger einen Angriffswert von 17 besitzt. Die einzelnen Balkenhöhen stellen die Wahrscheinlichkeiten dafür dar, mit welchem Zustand der Angreifer gewinnt. "100" steht für volle Gesundheit, "15" steht hier für "fast am Ende".- 100 Gesundheit
- 83 Gesundheit
- 66 Gesundheit
- 49 Gesundheit
- 32 Gesundheit
- 15 Gesundheit
- 0 oder weniger Gesundheit ist nicht möglich, andernfalls wäre der Angreifer besiegt, was aber der Voraussetzung, dass er den Kampf gewonnen hat, widerspricht.)
- Die in 3. eintretenden Kampfausgänge besitzen unterschiedliche Wahrscheinlichkeiten, aus denen sich dann hinterher die Siegeswahrscheinlichkeit zusammensetzt.
- Diese Wahrscheinlichkeiten werden durch die sogenannte Binominalverteilung ermittelt.
Die Binominalverteilung
Betrachten wir dazu das Modell des fortgesetzten Münzwurf.
Eine Münze wird 5-mal geworfen. Wie groß ist die Wahrscheinlichkeit, dass 3-mal die Zahl fällt?
Den 5-maligen Wurf der Münze können wir als eine Null-Eins-Folge interpretieren, wobei die Eins für das Ereignis steht, dass die Zahl fällt, die Null steht dann entsprechend für das Ereignis, dass Kopf fällt. Eine mögliche günstige Kette wäre dann z.B. 1-0-1-1-0.
Die Reihenfolge der Ereignisse ist egal, wichtig ist nur, wieoft die Eins oder die Null kommt.
Die Wahrscheinlichkeit, mit der aus dem 5-maligen Werfen 3-mal die Eins kommt, beträgt , wobei der Binominalkoeffizient ist.
Sei n die Länge einer Null-Eins-Folge. Die Wahrscheinlichkeit, mit der die Folge k-Einsen enthält, beträgt
, wobei p die Wahrscheinlichkeit dafür ist, mit der eine Eins fällt.
B(n,p,k) bezeichnet man dann als Binominalverteilung.
Formel für die Berechnung der Siegeswahrscheinlichkeit
Betrachten wir einen Kampf, bei dem der Angreifer gewinnt. Wie weiter oben beschrieben, können mehrere Ausgänge eintreten, was den Grad der Verletzung des Angreifers betrifft. Im Folgenden betrachten wir uns den Ausgang, dass der Angreifer unverletzt aus dem Kampf hervor geht. Das bedeutet, der Angreifer darf keine Kampfrunden verlieren, andernfalls würde er verletzt werden, was wir aber erstmal ausschließen.
Führen wir erstmal folgende Definition ein:
Definition
Seien und die Anzahl an Trefferpunkten des Angreifers bzw. des Verteidigers.
Die maximale Anzahl an Kampfrunden ergibt sich dann wie folgt:
(-1 deswegen, weil Angreifer und Verteidiger beide gleichzeitig den Kampf nicht verlieren können.)
Als Null-Eins-Folge interpretiert gilt: 1-1-1-...-1 , wobei die Eins dafür steht, dass der Angreifer die Kampfrunde gewinnt. Die Anzahl der Einser ist im diesem Falle gleich den Wert von .
Die Binominalverteilung darauf angewandt ergibt:
Dies ist die Wahrscheinlichkeit dafür, dass der Angreifer unverletzt den Kampf gewinnt.
Wird der Angreifer einmal getroffen, also er verliert genau eine Kampfrunde, dann gilt:
Warum und nicht ?
Hierzu betrachten wir uns die dazu gehörende Null-Eins-Folge: 1-1-...-0-...-1-1 . Die Folge enthält genau eine Null. Diese kann an einer beliebigen Stelle aufhalten, außer an der letzten. Die letzte Eins steht dafür, dass der Angreifer den letzten Treffer gegen den Verteidiger landet und ihn somit besiegt. Würde aber am Ende die einzige Null stehen, würde dass heißen, dass der Kampf nicht zu Ende wäre. Somit muss die letzte Stelle von einer Eins belegt sein. Als Konsequenz reduzieren sich automatisch die möglichen günstigen Anordnungen der Null-Eins-Folge.
(Zusammengefasst muss der letzte Treffer immer vom Angreifer kommen, wenn er siegen will.)
Wird der Angreifer zweimal getroffen, so gilt entsprechend:
Allgemein gilt nun für die Wahrscheinlichkeit, dass der Angreifer den Kampf gewinnt:
Der erste Summand ist gerade die Wahrscheinlichkeit, dass der Angreifer unverletzt den Kampf gewinnt, er also keine Kampfrunde verliert. Der zweite Summand steht dafür, dass der Angreifer genau eine Kampfunde verliert. Der letzte Summand steht dafür, dass der Angreifer Kampfrunden verliert, das bedeutet, dass er fast am Ende ist, eine weitere verlorene Runde würde einen Niederlage bedeuten. ( taucht nicht direkt in der Formel auf, es steht aber für die Anzahl aller Summanden.)
Definition:
Seien die Anzahl an Trefferpunkten des Angreifers bzw. des Verteidigers und seien die Wahrscheinlichkeiten dafür, dass der Angreifer bzw. der Verteidiger eine Kampfrunde gewinnt mit .
Dann gilt
- und
- ,
wobei für die Siegeswahrscheinlichkeit des Angreifers steht, den Kampf zu gewinnen, steht entsprechend für die Wahrscheinlichkeit eines Sieges des Verteidigers.
Berechnung der endgültigen Siegeschance ( mit Erstschlag)
Erstschläge
Als Erstschläge werden Kampfrunden bezeichnet, in denen eine Einheit, die Erstschläge zur Verfügung hat, nicht verletzt werden kann. Ansonsten sind sie mit den normalen Kampfrunden identisch. Allgemein gelten folgende Rahmenbedingungen für den Einsatz von Erstschlägen:
- Eine Einheit kann nur über Erstschläge verfügen, wenn sie mit entsprechenden Beförderungen (Erschlag I-V) ausgestattet wird oder sie bereits als Einheitenfähigkeit besitzt (z.B. besitzt der Bogenschütze einen Erstschlag).
- Besitzt eine Einheit Erstschläge, so hat sie eine gewisse Anzahl an "freien" Kampfrunden, in denen sie zwar wie gewohnt ihren Gegner verletzten kann, ohne aber dabei selber befürchten zu müssen, verletzt zu werden.
- Die Anzahl der "freien" Kampfrunden ist der Betrag aus der Differenz der Anzahl an Erstschlägen des Angreifers und der Anzahl an Erstschlägen des Verteidigers.
- "Freie" Kampfrunden kann nur entweder der Angreifer haben oder der Verteidiger, beide können nicht gleichzeitig während eines Kampfes "freie" Kampfrunden haben. Es ist auch möglich, dass es in einem Kampf keine "freie" Kampfrunden vorkommen. Dies ist genau dann der Fall, wenn Angreifer und Verteidiger die gleiche Anzahl an Erstschlägen besitzten.
- Es gibt Einheiten, die immun gegen Erstschläge sind, sei es durch Einheiteneigenschaft oder durch bestimmte Beförderungen. Auch in diesem Fall gibt es keine Kampfrunden.
- Erstschläge laufen vor dem eigentlichen Kampf ab. Theoretisch könnte bei einer ausreichend hohen Anzahl an verfügbaren Erstschlägen der Kampf gewonnen werden, ohne dass der Feind die Möglichkeit zur Gegenwehr hätte (was aber in der Praxis ein unwahrscheinlicher Fall ist).
Sei nun der Betrag von der Differenz aus den verfügbaren Erstschlägen des Angreifers und Verteidigers.
Weiterhin gilt:
1) Falls der Angreifer verfügt über -Erstschläge
2) Falls der Verteidiger verfügt über -Erstschläge
3) Falls Angreifer und Verteidiger verfügen über 0-Erstschläge
Endgültige Berechnung
Seien mit die Runde gemeint, mit der der Angreifer bzw. der Verteidiger den Kampf verliert und seien die Wahrscheinlichkeiten dafür, dass der Angreifer bzw. der Verteidiger den Kampf gewinnen, , sei die Anzahl der im Kampf eingesetzten Erstschläge.
Falls 1) zutrifft, dann gilt:
Falls 2) zutrifft, dann gilt:
Falls 3) zutrifft, dann gilt:
wobei , steht für die Wahrscheinlichkeit des Angreifers, beim -ten Erstschlag den Kampf zu gewinnen, steht für die Wahrscheinlichkeit des Verteidigers, beim -ten Erstschlag den Kampf zu gewinnen.
Weiterhin gilt:
wobei für die Siegeswahrscheinlichkeiten des Angreifers bzw. des Verteidigers stehen.
Zur Erläuterung der obigen Formeln befassen wir uns nur mit Fall (1). (Fall (2) geht vom Prinzip her analog, Fall (3) hatten wir schon weiter oben behandelt.)
Als Beispiel wählen wir . Dann gilt für den Angreifer:
Für den Verteidiger gilt:
Beispielrechnung
Zusätzliches